Fundamental Theorem of Calculus or short for FTC. Wow, it sounds scary and new, but it's all about the relationship between derivatives and integrals. FTC shows that derivates and integrals are indeed inverse of each other.
Real-world applications of derivatives: velocity, acceleration, optimization, etc.
Real-world applications of integrals: finding areas, accumulations, net changes, etc.
Part 1
Part one is about the formula that relates the derivative to the integral. If r(x) is continuous on [a,b] then
$$f(x)= \int_{a}^{x} r(t) \,dt$$
f(x) is continuous on [a,b], it is differentiable on (a,b) and
$$f'(x)=r(x)$$
Basically, if f(x) is an integral of r(x) then r(x) is a derivative of f(x).
It is like saying the square root of 4 is 2, then 2 squared is 4.

Before we move on to Part 2, let me give you an example. Try it yourself first and then move on to the explanation for better results.
In the next example, we are being asked to find the derivative of an antiderivative. The result should be the original function. In this problem, we have the last case from the table above. Step 4 is in every case. Why? Plugging in the endpoints gives you the initial and final accumulated quantities, allowing you to find the net change.
Plugging in the endpoints when evaluating a definite integral is a direct consequence of the FTC. The result obtained by plugging in the endpoints represents the net change or accumulation of the quantity represented by f(x) over the specified interval.
When the result of an integral is a function, the slope of that function represents the net change of the quantity being measured, and its positive or negative nature can be determined based on the slope's sign.
Net change: signifies how much a quantity has increased or decreased during that interval, taking into account all the positive and negative influences on the quantity (overall trend of net accumulation or net reduction of the quantity)
Example
$$f(x)= \int_{x^2}^{cos(x)} t^2+2 \,dt$$
Find f'(x).
$$f'(x)= (cos(x))^2+2-2x(x^4+2)$$
$$=-sin(x)(cos^2x+2)-2x(x^2+2)$$
The resulting function has a negative slope. What does that mean in the context of net change?
The function is decreasing as you move along the x-axis. When the rate of change is negative (negative slope), it indicates a decrease in the quantity (overall reduction in the quantity).
In real-world scenarios, a negative slope and negative net change could represent scenarios like decreasing temperature, declining population, decreasing stock prices, or decreasing levels of a substance.
General Formula
Here is a General Formula:
$$f'(x)= r[h(x)]*h'(x)-r[g(x)]g'(x)$$
h(x) : upper limit
g(x) : lower limit
Exercise
$$f(x)=\int_{2x^2}^{6} 6t^3-6t \,dt$$
Find f'(x).
Check your answer:
$$f'(x) = -192x^7+48x^3$$
Part 2
The second part of the theorem provides a way to compute definite integrals using antiderivatives. If we have a continuous function f(x) and its antiderivative F(x) on the interval [a, b], then the definite integral of f(x) from a to b can be calculated as the difference between the antiderivative evaluated at the endpoints:
$$\int_{a}^{b} f(x) \,dx= F(x)|_{a}^{b}=F(b)-F(a)$$
Both limits of integration must be constant. Also, the interval must be closed.
Example
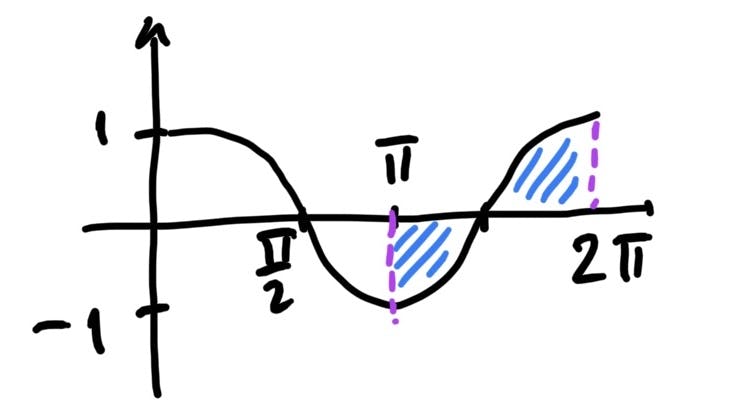
$$\int_{\pi}^{2\pi}cos\theta \, d\theta$$
and
$$F(x)=sin\theta$$
Solution:
$$F(b)=sin(2\pi)$$
$$F(a)=sin\pi$$
$$F(b)-F(a)=sin(2\pi)-sin(\pi)=0-0=0$$
We just found the net area (the area above the x-axis is the same as the area on the bottom)
Just like this: (Graph of Cosine)
Net Change Theorem (advanced*)
The Net Change Theorem is a concept closely related to the Fundamental Theorem of Calculus (FTC) and provides a practical way to compute net changes or accumulations of a quantity over a specific interval using definite integrals.
The Net Change Theorem states that the net change in a quantity over an interval [a, b] can be calculated by finding the definite integral of the rate of change of that quantity with respect to time over the same interval.
The Net Change Theorem states that if we integrate a rate of change of a function, we will find the net amount of the change of the function during the period of integration.
If f'(x) is the rate of change of f(x) then
$$\int_{a}^{b}f'(x) \, dx=f(b)-f(a)$$
Example
Water is being pumped into a tank at a rate ( gallons ) given by w(t) = 60 - 10√t, with 0 ≤ t ≤ 120 where t is the time in minutes since the purpling began. The tank had 1200 gallons of water in it when pumping began. Use the net change theorem to determine how much water will be in the tank after 49 minutes of pumping.
$$\int_{0}^{120} 60-10\sqrt{t}$$
The integral of the rate of change is the net change*.*
$$1200+\int_{0}^{49}60-10\sqrt{t} \,\,dt$$
Added the initial value of 1200 and we have a new interval [0,49]
$$1200+\int_{0}^{49}60-10t^{\frac{1}{2}} \,\,dt$$
$$1200+[60t-10*\frac{2}{3}t^{\frac{3}{2}}]_{0}^{49}$$
$$1200+[60*49-\frac{20}{3}49^{\frac{3}{2}}]-[0]=\frac{5560}{3}$$
About 1853.3 gallons of water will be in the tank after pumping 49 min.
Done!
Thanks for reading until the end. I have a Youtube Channel with some more Calculus content!
